同构图
的有关信息介绍如下：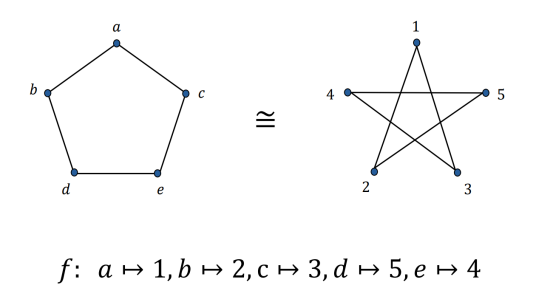
图论当中的术语，假设G=(V,E)和G1=(V1，E1)是两个图，如果存在一个双射m：V→V1，使得对所有的x,y∈V均有xy∈E等价于m(x)m(y)∈E1，则称G和G1是同构的，如图。
这样的一个映射m称之为一个同构，如果G=G1，则称其为一个自同构(automorphism)。
用符号𝑮 ≅ 𝑮′表示图同构。
图同构的直观即为，可以通过将图G的顶点重新标号，使之与图G'完全相同，则G与H同构。
想要了解更多“同构图”的信息，请点击：同构图百科
同构图
Simone
发布于 2024-10-02 18:31:12
574 阅读
